下面讲如何利用SAS Analysis 模块计算描述统计量、进行假设检验、拟合曲线以及进行回归分析
1.启动Analyst模块
选择Solutions菜单下的Analysis,然后再选择下面的Analyst,如图:
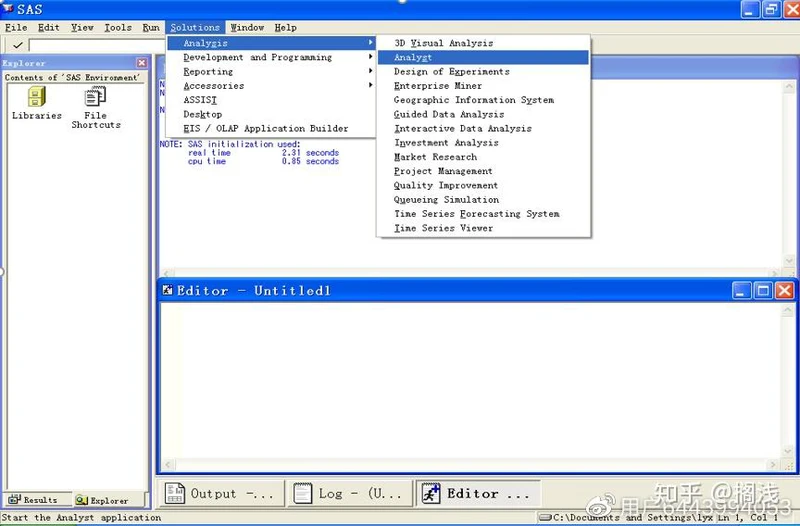
得到Analyst界面:
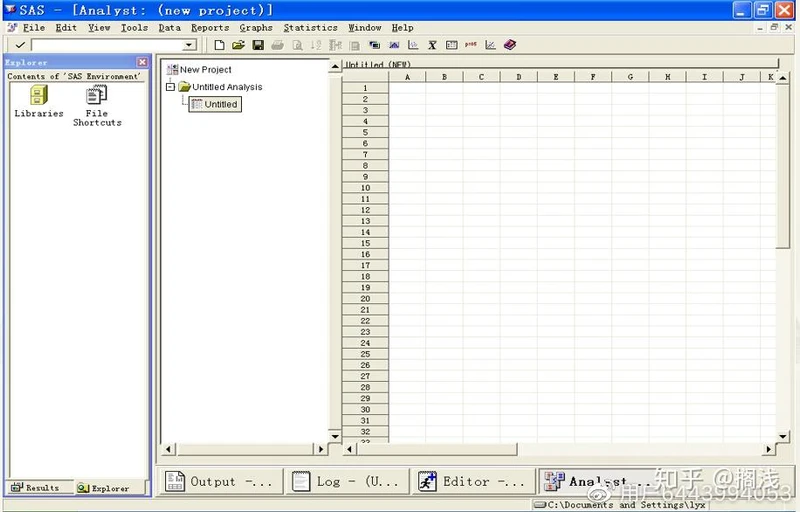
2.数据集相关操作
一、依分布产生数据
利用Data菜单中Random Variates可以产生服从特定分布的随机数,可以选择的分布类型包括:
* 正态分布
* 均匀分布
* 二项分布
* 卡方分布
* 泊松分布
* 指数分布
* Beta分布
* Gama分布
* 几何分布
* 极值分布
例1、利用Analyst模块生成100个服从标准正态分布的数据,并把生成的数据命名为Normal保存在Sasuser下。
操作步骤:
(1)在Data菜单中选择Random Variates,然后选择分布类型——Normal(正态分布),则弹出现一对话框:
(2)在Number of values to generate中填100,在New column name (变量名称)中填 X,在Mean中填0,在Standard deviation 中填1,单击OK
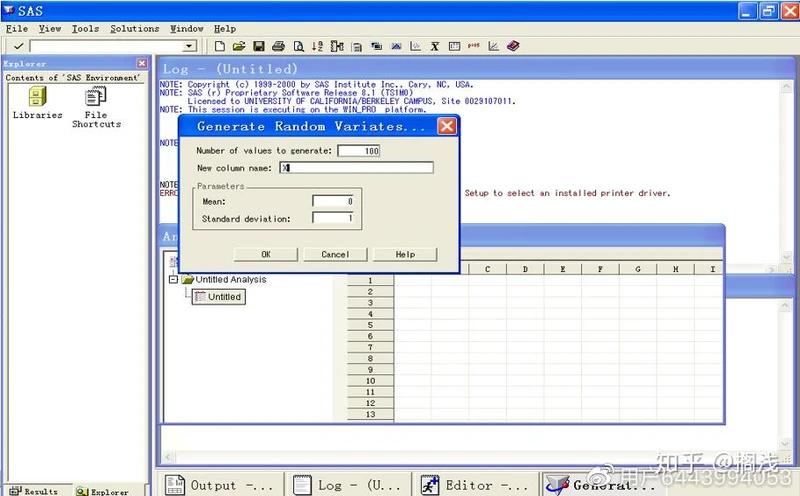
(3)可以看到数据集中产生了新的一列,在File菜单中选Save As By SAS Name,保存数据集
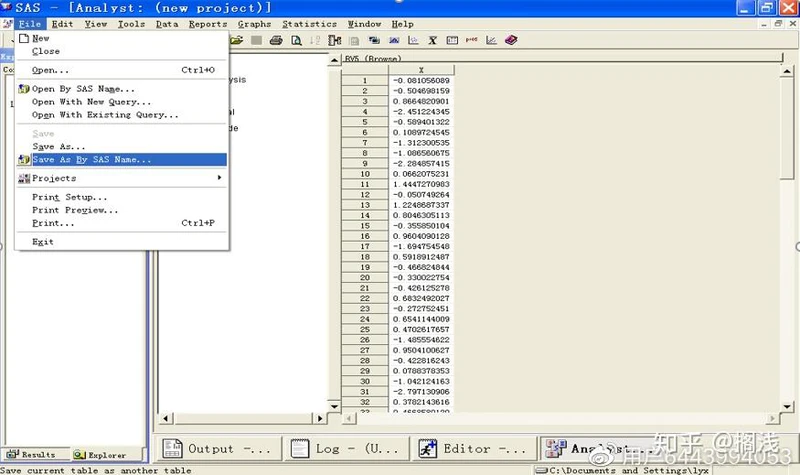
(4)在弹出的对话框中双击Sasuser,并在Member Name中填数据集名称 Normal,单击Save即可
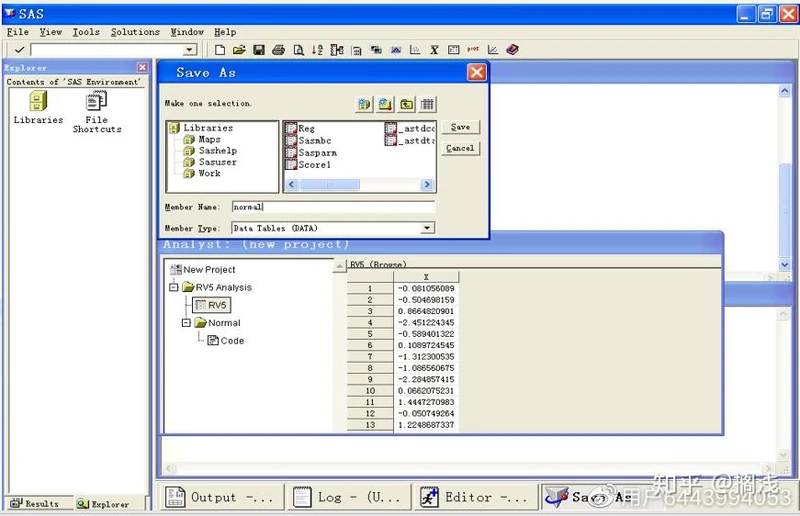
二、随机抽样
使用Data中Random Sample可以从数据集中随机抽取记录。
例:在刚才生成的正态数据集normal中随机抽取50个数据。
步骤如下:
(1)首先选择Data菜单下Random Sample命令,弹出对话框:
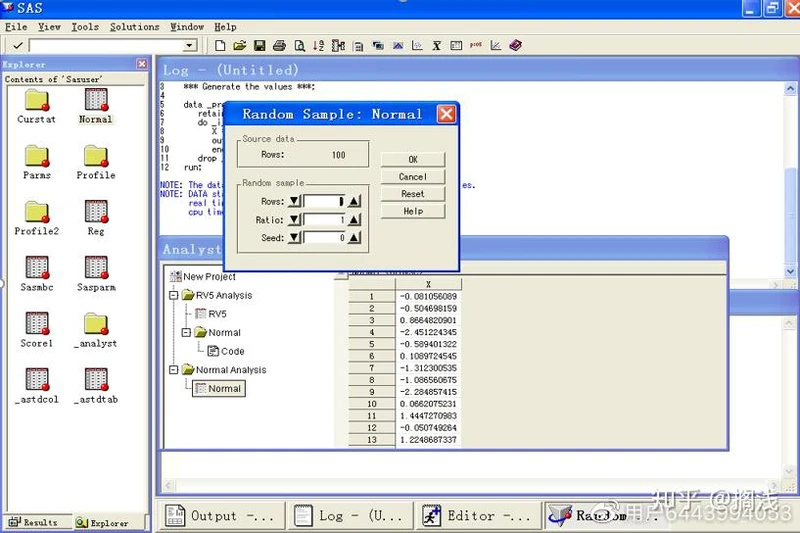
(2)在Rows中填50,单击OK即可得到一个表格含有随机抽取的50个样本,如图:
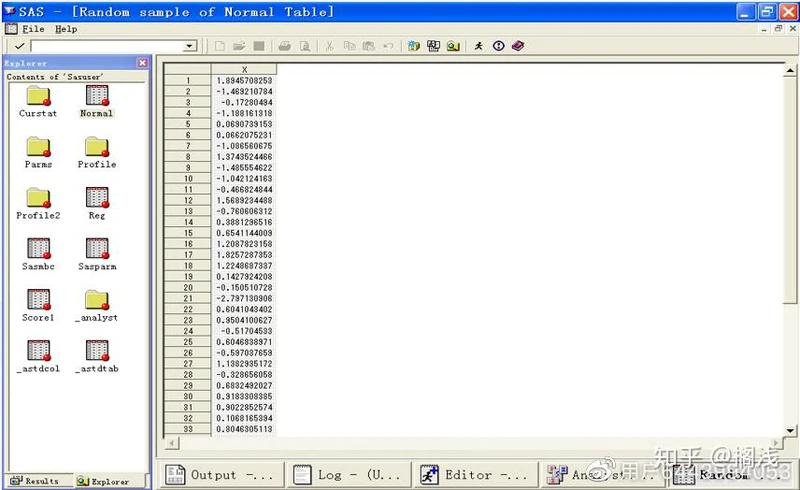
3.绘制统计图
一、绘制变量直方图并在图上拟合分布曲线
利用Grphs中Histogram可以绘制变量直方图并拟合分布曲线。
例:以上节normal数据集中X为对象绘制直方图,并在直方图上拟合正态分布曲线。
操作步骤:
(1)打开Normal文件:File→Open By SAS Name→Sasuser→Normal→OK
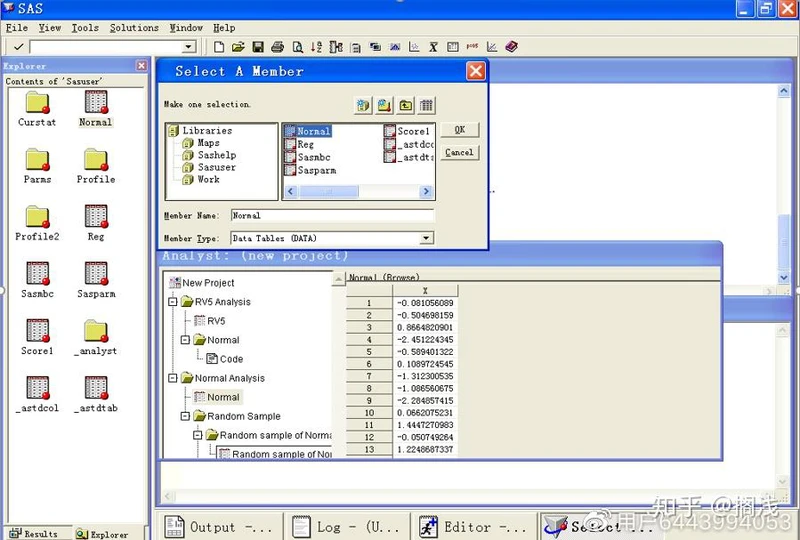
(2)在Grphs下选Histogram,单击绘图变量X,再单击Analysis将其加入
(3)选择Fit在直方图上拟合正态分布曲线,单击Fit弹出对话框
(4)选择Normal,单击OK回到原对话框,再单击OK即得:
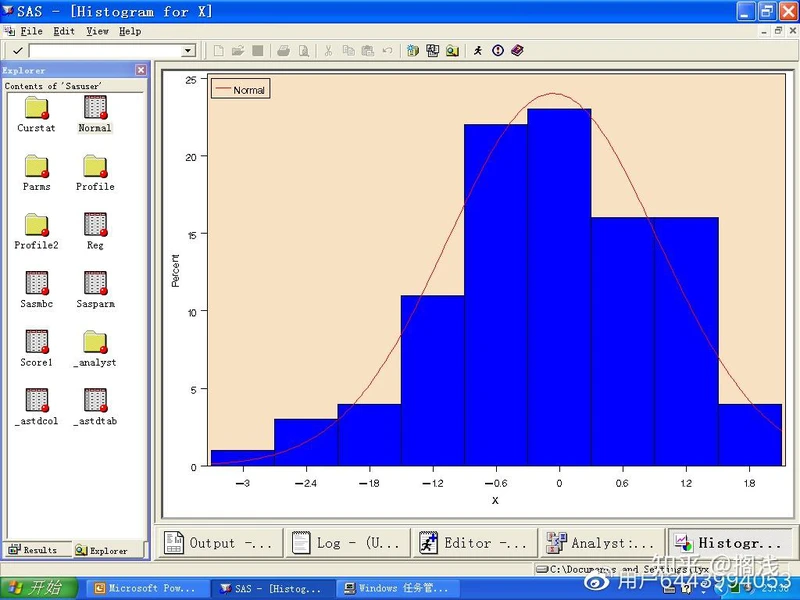
二、概率图
在直方图基础上我们可以猜想变量是服从正态分布的,通过绘制概率图可以来证实我们的想法。概率图将数值排序,给出每个数值对应的分位数,然后打点作图。如果这些点呈现线性特征,说明他们与理论分布相符,同时又在图像上加上一条给定分布的曲线,并给出分布的系数。
例:绘制Normal数据集中X的概率图,步骤如下:
(1)首先选择Graphs下Probality Plot,弹出对话框
(2)单击X,再单击Analysis,然后选择分布为Normal,单击Ok得到概率图:
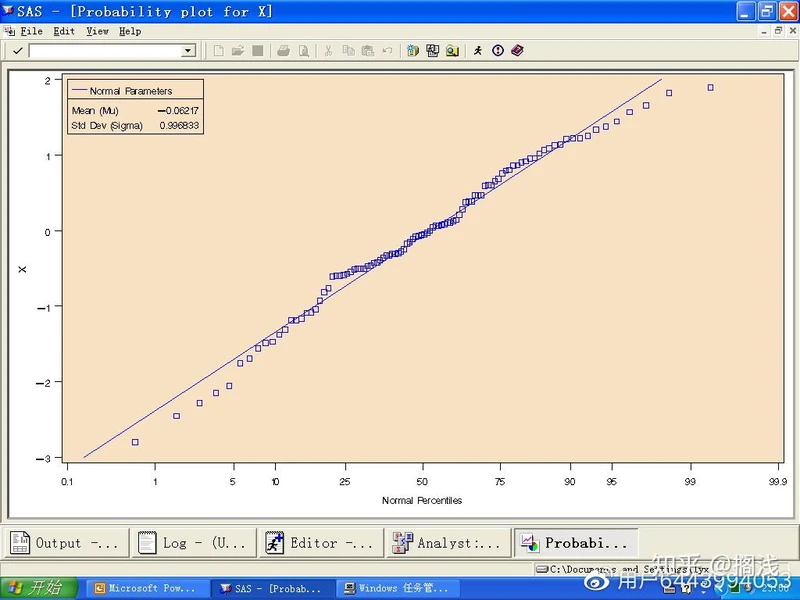
可以看到X的分布与正态分布基本吻合,图中还给出了正态分布的参数:均值为-0.06217,标准差为0.996833。
一、绘制散点图
使用Graphs下的Scatter Plot可以绘制散点图
例:病人在服用某种放射性药物后,体内的放射性物质的含量y与时间x具有一定的关系,绘制二者的散点图,然后找出他们的关系,数据如下:

1、首先将数据输入建立一个名为Test的数据集,然后在ANALYST模块下打开
2、然后打开Scatter Plot对话框
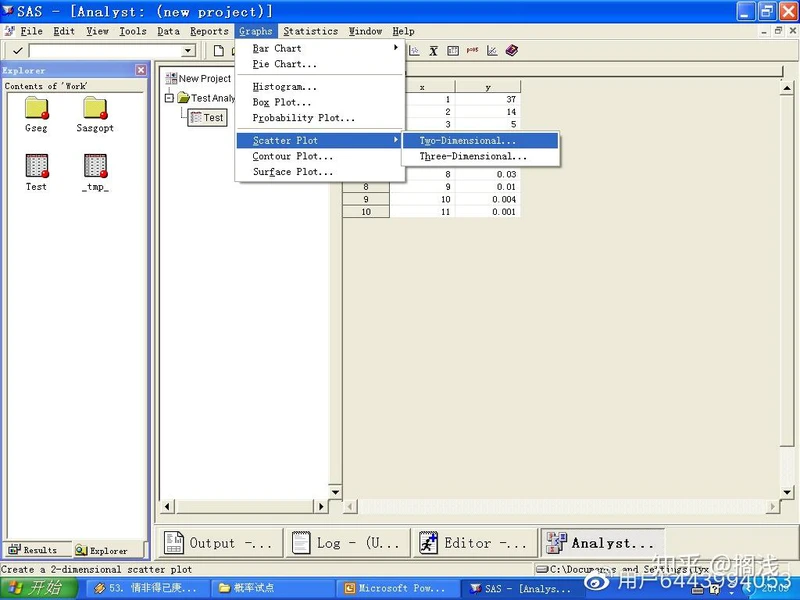
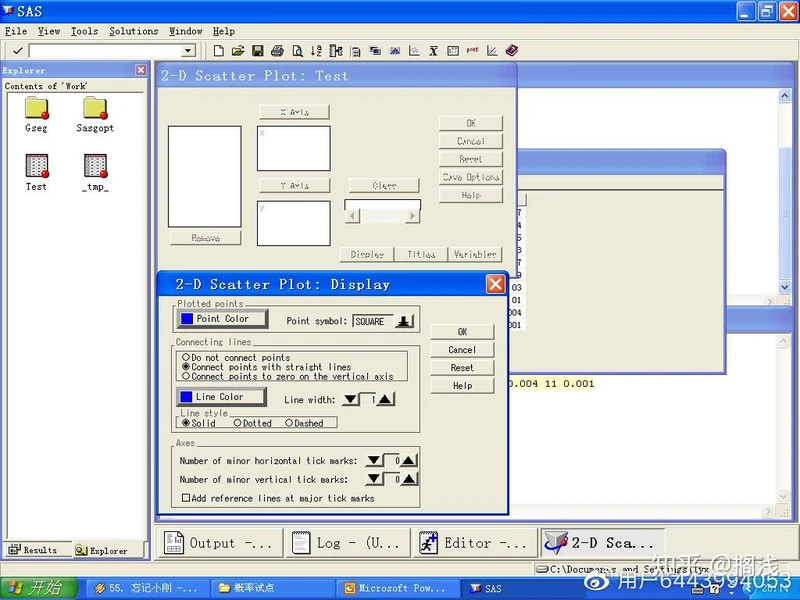
3、在绘制散点图对话框中将x放在X轴,y放在Y轴,单击OK可以得到二者的散点图,为容易观察,可在Display中选择用线连接散点图
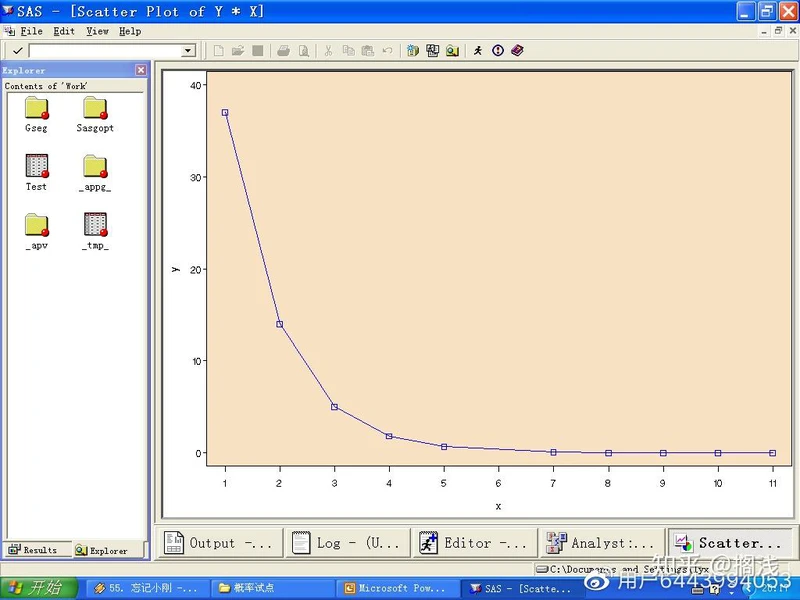
4、绘制的图形如下,可以看到放射性物质的含量和时间具有负指数衰减关系
4.回归分析
利用Statistics菜单下的Regression可以进行回归分析,包括:
* Simple回归:单一的自变量,单一的因变量,但自变量次数可以是一次、二次或三次
* Linear回归:多个自变量,多个因变量,但是对因变量分别进行回归
一、Simple回归
例:大量父亲身高x与儿子身高y的资料,其中10对数据如下:
X 60 62 64 65 66 67 68 70 72 74
Y 63.6 65.2 66.0 65.5 66.9 67.1 67.4 68.3 70.1 70.0
假设对给定的x, y为正态变量,且方差与x 无关,求回归方程y=a + bx,并指出回归效果是否显著。(显著水平取0.05)
程序语句:
1、首先建立数据集:
data sasuser.reg;
input x y@@;
cards;
60 63.6 62 65.2 64 66.0 65 65.5 66 66.9 67 67.1 68 67.4 70 68.3 72 70.1 74 70.0
;
run;
2、再利用菜单完成回归分析:
(1) 选择Solutions→Analysis→Analyst菜单,
(2) 选择File→Open By SAS Name→sasuser→reg
(3) 选择Statistics→Regression,
(4) 选择Simple Linear Regression出现一窗口
3、在出现的窗口中设置变量,我们选择变量dependent为y,选择Explanatory为x, Model处选择Linear, Tests按钮可以选择显著性水平,默认是0.05。
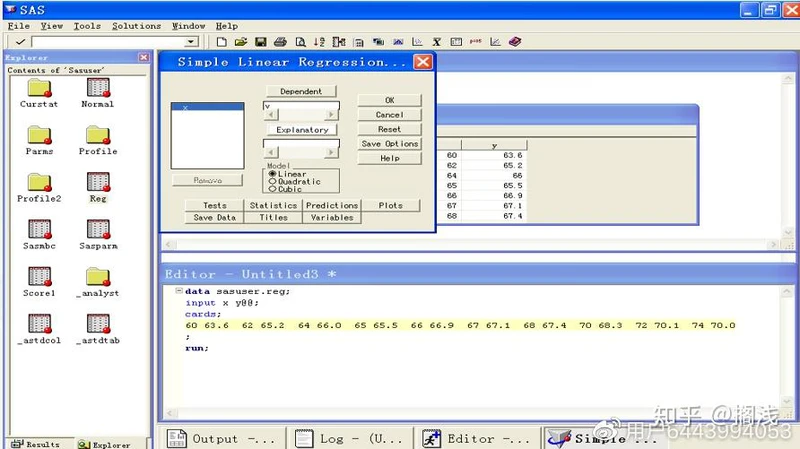
4、单击OK,产生输出结果
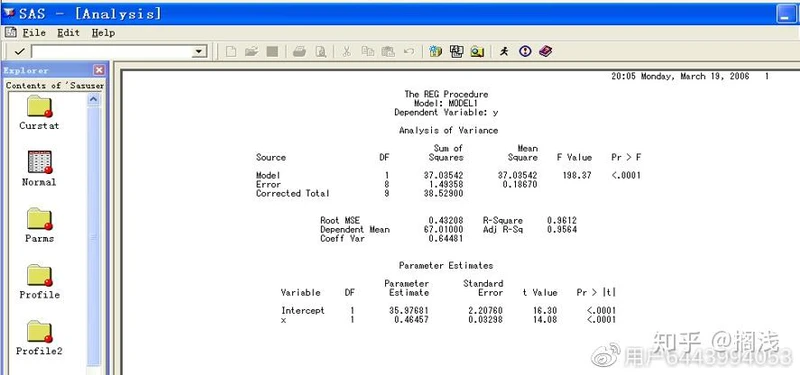
5、首先由模型的方差分析表可以看到, Prob > F 的值为0.0001<α=0.05,因此该回归方程显著,再由下面的参数估计可以得出回归方程为:
y=35.97681+0.46457x
二、Linear回归
例2:外贸数据分析
1、首先建立数据集
data reg;
input n x1-x3 y@@;
cards;
1 149.3 4.2 108.1 15.9 2 161.2 4.1 114.8 16.4
3 171.5 3.1 123.2 19.0 4 175.5 3.1 126.9 19.1
5 180.8 1.1 132.1 18.8 6 190.7 2.2 137.7 20.4
7 202.1 2.1 146.0 22.7 8 212.4 5.6 154.1 26.5
9 226.1 5.0 162.3 28.1 10 231.9 5.1 164.3 27.6
11 239.0 0.7 167.6 26.3
;
run;
2、再利用菜单完成回归分析:
(1) 选择Solutions→Analysis→Analyst菜单,
(2) 选择File→Open By SAS Name→work→reg
(3) 选择Statistics→Regression,
(4) 选择 Linear Regression出现一窗口
(5) 在出现的窗口中设置变量,我们选择变量dependent为y,选择Explanatory为x1,x2,x3, Tests按钮可以选择显著性水平,默认是0.05。
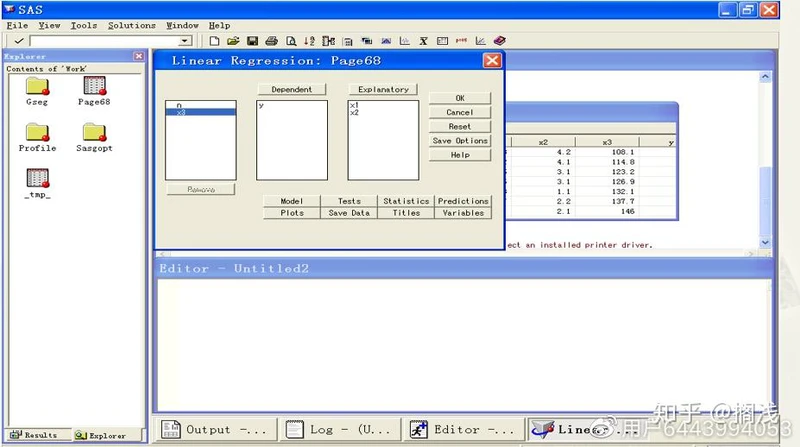
3、单击OK产生结果
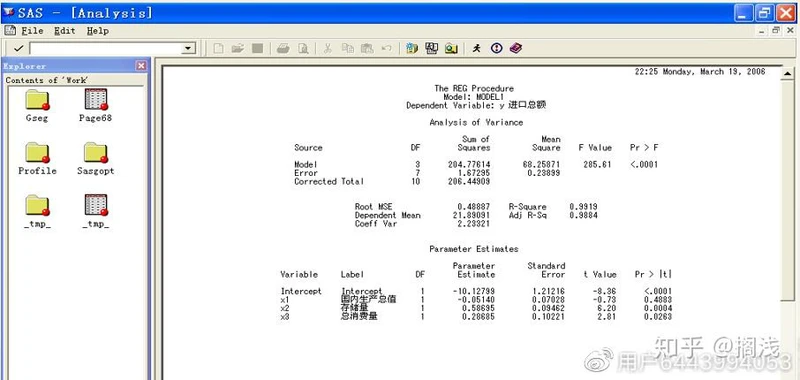
4、首先由模型的方差分析表可以看到, Prob > F 的值为0.0001<α=0.05,因此该回归方程显著,再由下面的参数估计可以得出回归方程为:
y=-10.13-0.05x1+0.59x2+0.29x3
但从数表来看,随着国内生产总值(X1)的增加进口总额(y)也增加,所以该方程并不一定是真实的反映了他们间的关系,进一步的探讨需要专门的回归分析理论,在此不作进一步讨论,此例只是想给大家一个抛砖引玉的作用。


