统计学习
2.1 什么是统计学习?
The inputs go by different names, such as predictors, independent variables, features, or sometimes just variables. The output variable — in this case, sales — is often called the response or dependent variable, and is typically denoted using the symbol Y .
输入有不同的名称,如预测器、独立变量、特性,有时甚至只是变量。输出变量——在本例中是sales——通常被称为响应变量或因变量,通常使用符号Y表示。
2.1.1 为什么估计f
- Prediction
通用形式
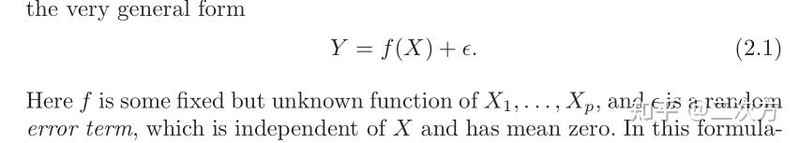
- 可约误差和不可约误差
- 可约误差 reducible error:这个误差是可以减少的,因为我们可以潜在地提高ˆf使用最合适的统计学习技术来估计f。
- 不可约误差 irreducible error:这就是所谓的不可约误差,因为无论我们估计f有多好,我们都无法减少ε所引入的误差。
- Inference 推断
弄清楚X和Y的关系,现在ˆf不能被视为一个黑盒,因为我们需要知道它的确切形式。 - 感兴趣的问题
- Which predictors are associated with the response?
- What is the relationship between the response and each predictor?
- Can the relationship between Y and each predictor be adequately summarized using a linear equation, or is the relationship more complicated?
- 根据我们的最终目标是预测、推理还是两者的结合,估计f的不同方法可能是合适的。
2.1.2 我们怎样估计 f
- training data:这些观察结果被称为训练数据,因为我们将使用这些观察结果来训练,或者教我们如何估计f的方法。
- 参数与非参数:parametric or non-parametric
- Parametric methods
- 参数化方法包括两步基于模型的方法。
- 1)对f的函数形式或形状作一个假设。
- 2)在选择了一个模型之后,我们需要一个使用训练数据来拟合或训练模型的过程。
- 刚才描述的基于模型的方法被称为参数化;它将f的估计问题简化为一组参数的估计问题。
- 一些复杂的模型可能会导致一种被称为数据过拟合的现象,这本质上意味着它们过于接近误差或噪声而进行过拟合。
- Non-parametric methods
- 非参数方法:非参数方法不明确地假设f的函数形式。相反,它们寻求f的估计,在不太粗糙或不太摇摆的情况下,尽可能接近数据点。
- 优点:通过避免假设f的特定函数形式,它们有潜力准确地拟合f的更大范围的可能形状
- 缺点:由于它们没有将估计f的问题减少到少量的参数,为了获得f的精确估计,需要非常大量的观测(远远超过参数方法通常需要的)。
- 非参数方法中的数据过拟合:这是我们之前讨论过的数据过拟合的一个例子。这是一种不希望出现的情况,因为所获得的拟合将不会对不属于原始训练数据集的新观察结果的响应产生准确的估计。
2.1.3 预测精度和模型可解释性之间的权衡
- 使用不同的统计学习方法,在灵活性和可解释性之间权衡的表示。通常,当方法的灵活性增加时,其可解释性就会降低。
- 当推理是目标时,使用简单和相对不灵活的统计学习方法有明显的优势;当预测是目标时,适应灵活和复杂的方法更有优势。
- 令人惊讶的是,情况并非总是如此!使用一种不太灵活的方法,我们通常会获得更准确的预测。这一现象乍一看似乎有悖直觉,它与高度灵活的方法中可能存在的过度拟合有关。
2.1.4 监督学习与非监督学习
- 监督学习:对于预测器测量(s) xi的每次观测,i = 1,…,有一个相关的响应测量yi.
- 非监督学习:无监督学习描述的是更具挑战性的情况,在这种情况下,对于每个观察i = 1,…,n,我们观察到一个测量向量xi,但没有相关的响应yi. 例如聚类分析方法。
- 半监督学习问题。
2.1.5回归与分类问题
- 定量变量和定性变量
- 我们倾向于把具有定量反应的问题称为回归问题,而那些涉及到定性反应的问题称为分类问题
- 然而,分类的区别并不总是那么清晰。最小二乘线性回归用于定量响应,而逻辑回归(第4章)通常用于定性响应。
- 预测因子是定性的还是定量的通常被认为不那么重要。本书中讨论的大多数统计学习方法都可以应用,无论预测变量的类型如何,只要在分析执行之前对任何定性预测变量进行了适当的编码。
2.2 评估模型精确度
2.2.1 测量适合度的质量
为了评估统计学习方法在给定数据集上的性能,我们需要某种方法来衡量其预测与观测数据的实际匹配程度。
- 均方误差 mean squared error (MSE)
- 在回归设置中,最常用的测量方法是均方误差。
- 如果预测的响应与真实的响应非常接近,则均方误差较小;如果某些观测的响应与预测的响应相差很大,则均方误差较大。
- 公式
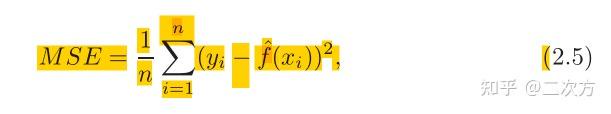
- 训练均方误差和测试均方误差
- 有测试数据集时,寻求测试均方误差最小;没有测试均方误差时,寻求训练方差最小。
- 不幸的是,上述第二种策略有一个基本问题:不能保证训练MSE最低的方法也会有最低的测试MSE。
- 普遍规律:随着统计学习方法灵活性的增加,训练MSE呈单调下降趋势,测试MSE呈u形变化。

- 数据过拟合:当一个给定的方法产生一个小的训练MSE但一个大的测试MSE时,我们被称为数据过拟合。
2.2.2偏差-方差权衡
- 对于给定的值 x_0 ,期望检验MSE总是可以分解为三个基本量之和:ˆf( x_o )的平方偏差ˆf( x_o)和误差项ε的方差。
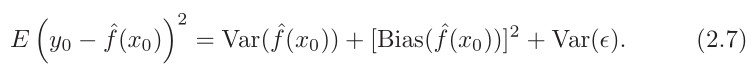
- 公式2.7告诉我们,为了使期望测试误差最小化,我们需要选择一种同时达到低方差和低偏差的统计学习方法。
- 方差
- 方差指的是如果我们使用不同的训练数据集来估计ˆf,它将会改变
- 一般来说,统计方法越灵活,方差越大
- 偏差
- 偏差是指用一个简单得多的模型来逼近一个可能极其复杂的现实问题时所产生的误差
- 一般来说,当我们使用更灵活的方法时,方差会增加,偏差会减少。
- 偏差-方差权衡
- 如图2.12所示,式2.7所示的偏差、方差和测试集MSE之间的关系称为偏倚-方差权衡
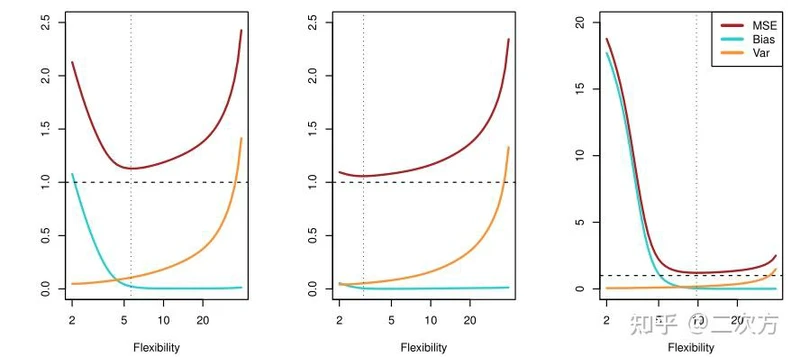
- 这被称为一个权衡,因为它很容易获得一个以极低的偏差但高方差的方法(例如,通过绘制曲线,通过每一个训练观察)或一个方法非常低方差高偏差(通过拟合数据)的水平线。
- 挑战在于找到一种方差和平方偏差都很低的方法。这种取舍是本书中反复出现的最重要的主题之一。
2.2.3分类设置
- 错误率:量化估计f的准确性最常见的方法是训练错误率,即如果我们将估计f应用于训练观察,所产生的错误的比例

- 训练错误率和测试错误率
- 贝叶斯分类器
- 在一个只有两个可能响应值的两类问题中,假设是class 1或class 2,当Pr(Y = 1|X = x_o ) >0.5时,选择类1,反之类2。
- 紫色虚线表示概率恰好为50%的点。这叫做贝叶斯决策边界
- 贝叶斯错误率:贝叶斯分类器产生最低的测试错误率,称为贝叶斯错误率。
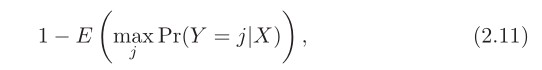
- 贝叶斯错误率类似于前面讨论的不可约误差。
- 理论上,我们总是喜欢使用贝叶斯分类器来预测定性反应。但对于真实的数据,我们不知道Y给定X的条件分布,因此计算贝叶斯分类器是不可能的。
- k近邻分类器(KNN)
- 给定一个正整数K和一个测试观测x_o , KNN分类器首先识别出训练数据中最接近x_o 的K个点,用 n_0 表示。然后估计第j类的条件概率为n_0 中响应值为j的点的分数:
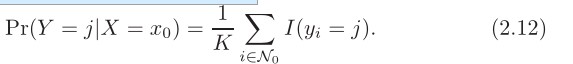
- 最后,KNN应用贝叶斯规则,将测试观测 x_0 分类到概率最大的类。
- 就像在回归设定中一样,训练错误率和测试错误率之间并没有很强的关系
- 在图2.17中,我们将KNN测试和训练误差绘制为1/K的函数。随着1/K的增加,方法变得更加灵活。在回归设置中,训练错误率随着灵活性的增加而下降。然而,当方法变得过于灵活和过拟合时,测试误差呈现出u型特征,首先下降(在K = 10左右有一个最小值),然后再次增加。

本学习笔记整理参考于Gareth James等学者编写的《An Introduction to Statistical Learning With Applications in R》。


